Developing retro games is always a dance of balancing features, processing speed, and cartridge space. Sloppy code or unrefined design can lead to a sloppy, slow game. However, the clever design and masterful code can create a beautifully choreographed game. Programming the behavior of Voracious Ghosts in the Meating is an example of one such dance of development and design.

The Hungriest Meat

If you played platformers, then you probably noticed that almost every game of this genre has one thing in common: enemies. Enemies vary from game to game, but they all have the ability to attack us at the most inconvenient moment, creating additional gameplay difficulties.

Some enemies are pretty stupid, like these Contra soldiers. They only follow along with the platform in one direction, so the player must shoot them, or avoid colliding with them, so as not to lose precious life.

However, the logic of some enemies may be a bit more complicated. Complex enemies, with special patterns, abilities, or behavior present players with an added challenge, and forces them to use their knowledge of the player character and the game world. Case in point is the behavior, and weaknesses, of the Voracious Ghost from The Meating.

This hungry spectre patrols the platform, and if a player comes too close to them, they will smell the bovine meat and rush in to attack:

It works quite simply. If the distance is more than 64 pixels (4 metatiles of 16 pixels each), the ghost will continue to move. But if the distance between the player is reduced to four or fewer metatiles, the ghost will switch to attack mode. We could do it like this:

if (playerX > ghostX)

 

else

if (distance <= 64)

Ghost.status = GHOST_ATTACK;

But it seems we did not take into account something else.

Hiding the Meat

To give our enemies more realism, we must endow it with vision. And if there is a block or platform between the player and the ghost, the ghost will not “see” the player and will not attack him. Take a look for yourself:

What should we add to our math to allow the player to hide behind the blocks?

First, let's understand how the level map works.

Our game map is divided into metatiles. Look at this picture above: there are 16 columns and 15 rows that form 240 cells. In each of these cells, there is a metatile - a “piece of graphics” 16x16 pixels in size.

In turn, metatiles can be solid and not solid. Solid metatiles are platforms, walls, floors. In a word, those graphic elements that the player and other creatures of our game world are not allowed to pass through. I marked these metatiles with green rectangles.

The remaining metatiles are not solid and have no collision. These are just the elements of the background, wallpaper, and other elements of the interior through which the player and the monsters are allowed to pass.

Let's return to our ghost. Suppose the X coordinate of our minotaur is 96. The ghost is at position 160.

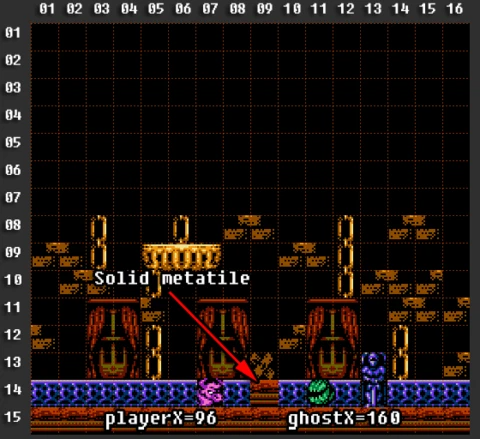
Let's calculate the distance between them:

distance = 160 - 96 = 64.

But among other things, we must consistently check every metatile between the ghost and the player. I highlighted these metatiles in the picture below.

And if at least one of the metatiles is solid, we must prohibit the ghost from attacking the player.

It might look like this:

// Reset playerDetected variable

playerDetected = 0;

distance = ghostX - playerX; // 160 - 96 = 64

So, the distance between the player and the ghost is 4 metatiles or 64 pixels. This is enough to start the attack, but we still haven’t checked the metatiles between the player and the ghost. Well, let's remedy that straight away.

if (distance <= 64)

{

 

}

}

 

if (playerDetected)

Ghost.status = GHOST_ATTACK;

As you can see, nothing complicated.

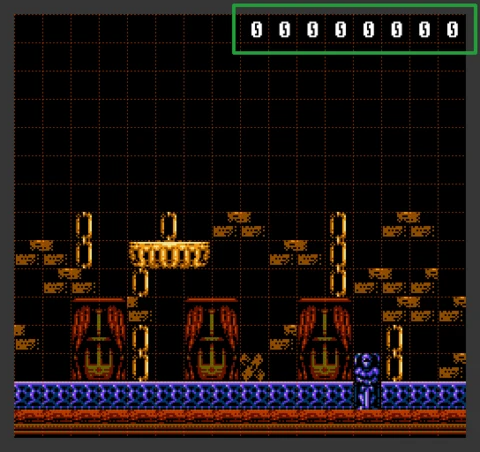
However, we did not think about how quickly such mathematics would work. Let's measure the speed of these calculations.

I added this gray debugging bar to see how many CPU cycles there are left in the current frame. The lower this bar is, the fewer processor cycles per frame we have left. We must not allow this bar to move beyond the bottom edge of the screen, otherwise, we will get a lag.

Notice that at the moment when an enemy spotted a player, this bar shifts down by ~30 pixels. This is the very load that the CPU receives during the calculation of the distance, taking into account the verification of solid metatiles. If there is not one enemy on the screen, but two, or three, such calculations will give even more load on the processor.

Can we speed up these calculations? Yes, we can!

Tightly Canned Meat

First of all, we have to get rid of the use of loops and check just two bytes instead of three, four, five, etc (depending on the distance). We also need a cache of 30 bytes.

unsigned char cacheMap[30];

One byte contains 8 bits, so let's group 8 metatiles into one byte. If the metatile is solid, we set the corresponding bit to 1. If the metatile is not solid, we will leave 0 here.

The first 8 metatiles in our map are empty, so these are 8 zero bits in a row. If we convert it to a decimal format, we get 0. Let's store this byte to the cache:

cacheMap[0] = 0;

Let’s proceed to the next byte.

Here, 0, too, oddly enough, so

cacheMap[1] = 0;

The next 7 rows (or 14 bytes) will also be zero.

cacheMap[2] = 0;

cacheMap[3] = 0;

cacheMap[4] = 0;

cacheMap[5] = 0;

cacheMap[6] = 0;

cacheMap[7] = 0;

cacheMap[8] = 0;

cacheMap[9] = 0;

cacheMap[10] = 0;

cacheMap[11] = 0;

cacheMap[12] = 0;

cacheMap[13] = 0;

cacheMap[14] = 0;

cacheMap[15] = 0;

But in the eighth row of our map, there is a platform.

0000 1110 bin = 14 dec, so

cacheMap[16] = 14;

In the end, we will reach the bottom row:

1111 1111 bin = 255 dec.

cacheMap[28] = 255;

cacheMap[29] = 255;

It seems, our cache is ready.

We do not need to fill the cache manually, so we can write a subroutine for every situation.

unsigned char cacheMap[30];

const unsigned char cacheMask[8] = { 128, 64, 32, 16, 8, 4, 2, 1 };

void makeLevelCache (void)

{

 

 

 

cacheBit = cacheMask[i & 7];

}

}

Let's move on.

Suppose our character is in the sixth cell of the map, a ghost in the eleventh cell. And in the eighth and ninth cells are solid metatiles.

To check the presence of an obstacle, we need to work a little with the first byte of the cache, which is 1 (0000 0001 binary).

We need to maintain only those bits that are to the right of the player, and we will reset the remaining bits. Let's apply boolean algebra for this:

0000 0001 AND 0000 0011 = 0000 0001 (1)

For the second half of the screen, the rules will be slightly different, we will save the bits to the left of the ghost, and reset the remaining bits:

1000 0000 AND 1100 0000 = 1000 0000 (128)

As we can see, nothing has changed. Both the left and right cache bytes are not zero. So, there is an obstacle there.

Let's try to move the first solid metatile from the eighth cell to the fifth, and the second solid metatile from the ninth cell to the thirteenth, and see what happens.

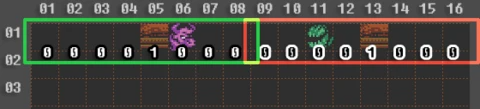
0000 1000 AND 0000 0011 = 0000 0000 (0)

And second byte:

0000 1000 AND 1100 0000 = 0000 0000 (0)

It seems our theory works! As a result of these operations, we got zeros, which means that no bits are set to the right of the player and to the left of the ghost. So you have to run, otherwise, you are attacked by a ghost, because nothing prevents you from doing it - there are no solid metatiles.

Now, let’s try to write the code. This code will be fully functional only for the special case when the player and the enemy are in different halves of the screen. But this will be enough to discover how it works.

First, we will prepare masks for the left and right sides of the screen:

// leftMask - 0..127 array containing left side masks

// where x 0..15 mask = 0111 1111 = 127;

// where x 16..31 mask = 0011 1111 = 63;

// where x 32..47 mask = 0001 1111 = 31;

// where x 48..63 mask = 0000 1111 = 15;

// where x 64..79 mask = 0000 0111 = 7;

// where x 80..95 mask = 0000 0011 = 3;

// where x 96..111 mask = 0000 0001 = 1;

// where x 112..127 mask = 0000 0000 = 0;

const unsigned char cacheLeftMask[] = {

127,127,127,127,127,127,127,127,127,127,127,127,127,127,127,127,

63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,

31,31,31,31,31,31,31, 31,31,31,31,31,31,31,31,31,

15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,

7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,

3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,

1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,

0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0

};

// rightMask - 0..127 array containing right side masks

// where x 0..15 mask = 0000 0000 = 0;

// where x 16..31 mask = 1000 0000 = 128;

// where x 32..47 mask = 1100 0000 = 192;

// where x 48..63 mask = 1110 0000 = 224;

// where x 64..79 mask = 1111 0000 = 240;

// where x 80..95 mask = 1111 1000 = 248;

// where x 96..111 mask = 1111 1100 = 252;

// where x 112..127 mask = 1111 1110 = 254;

const unsigned char cacheRightMask[] = {

0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,

128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,

192,192,192,192,192,192,192,192,192,192, 192,192,192,192,192,192,

224,224,224,224,224,224,224,224,224,224, 224,224,224,224,224,224,

240,240,240,240,240,240,240,240,240,240,240,240,240,240,240,240,

248,248,248,248,248,248,248,248,248,248,248,248,248,248,248,248,

252,252,252,252,252,252,252,252,252,252,252,252,252,252,252,252,

254,254,254,254,254,254,254,254,254,254,254,254,254,254,254,254

};

And now we will write a subroutine:

unsigned char checkDistance (unsigned char maxDist)

{

unsigned char distance, cachePos, playerResult, enemyResult;

const unsigned char* maskTable;

 

 

 

 

 

enemyResult = !(cacheMap[cachePos] & maskTable[enemyX & 0x7f]);

}

}

Still don't get it? It's ok, let's just recap:

• We have only 16 cells horizontally where a player and an enemy can be.
• For each of these cells, we have a unique mask byte, which we obtain from a pre-calculated table. If at least one of the comparison results (for a player or an enemy) is positive, and the distance between the characters is within the required limits, we can say for sure: an obstacle is there.

Okay, let’s compile it.

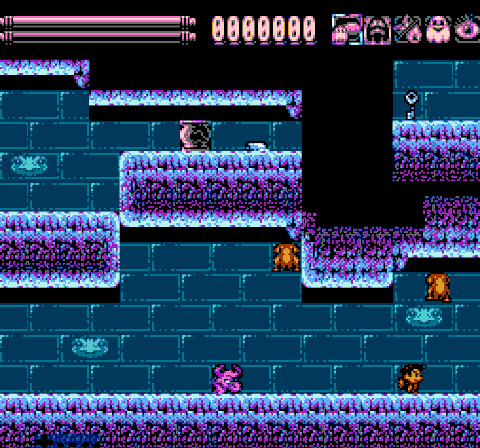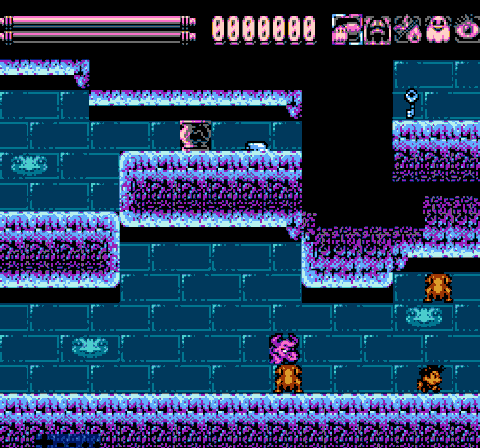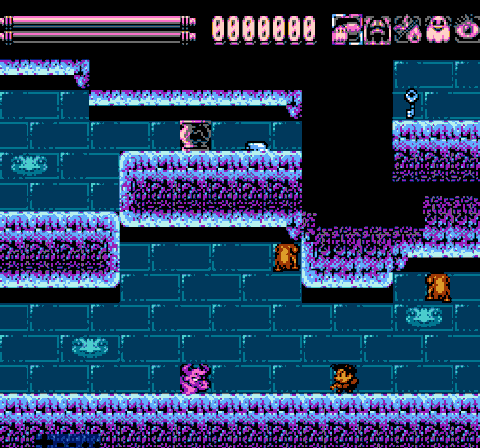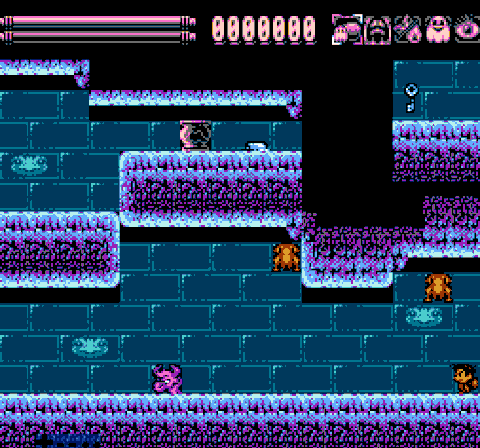
Job is done! Now we have to perform the test once again.

Obviously, this method is much faster than to sort through each metatile between the enemy and the player. Of course, we have to spend 256 bytes to store these two tables in PRG-ROM. But you must admit, it's worth it. Our meat is packed to UoROM cart with 256KiB of ROM, so I can afford it. In addition, the size of these tables can be greatly reduced, but this will add some more calculations. I choose speed. Decide for yourself what your balance should be.

Now, we can add a few more enemies to the screen, cause we have enough CPU cycles for all the calculations.

No go forth and have a good retro coding session!

 

Want more tips straight from the retro pros? Welcome to our Discord!

Get mad meat on The Meating page now!